意图 在 Win10、Win11 下，实现一个具有类似 MacOS 下 TotalSpace 功能的程序。 市面上免费的、收费的程序有不少，但都有不尽如人意的地方，尝试自行实现。 Q：为什么只支持 Win10、Win11？ A：Win10、Win11 系统中的虚拟桌面 (Virtual Desktop)，是新加入的机制，强调：轻量级与灵活/便利性。较之传统的通过调用 CreateDesktop 生成的桌面，实现某些功能时更加简单直接。详见后文。 原则与限制 既可以由程序完全控制所有桌面（这是 Dexpot 的实现方式），也可以封装并增强系统自带的虚拟桌面。综合考量程序的资源占用、性能、稳定性、兼容性、系统/代码库依赖、打包大小、扩展 …

阅读更多

描述 能为静态站点提供评论功能的第三方模块有很多(排名无先后) Disqus Talkyard HyperComments Remarkbox IntenseDebate Gitalk Gitment Vuukle Muut 且都各有其优缺点。要取舍这些模块，先明确功能与特性的需求： 免费 无广告 高度定制 评论信息保存在站点所有者可控的存储介质中 安全 迁移成本低 经过筛选，决定使用 staticman 该系统可以满足上述需求，唯一的缺点是部署步骤较多，因此撰写此文，方便参考 本文专注：无(低)成本的让 staticman 在 Hugo 中运行，因此诸如 Hugo 的安装配置，相关站点的注册等则省略 涉及应用 Name …

阅读更多

TL;DR 首先，确未想到，为说清楚这个玩意儿，居然要用不少的篇幅；其次，当涉及对一些概念、原理的追溯时，递归到多深的地步，也不容易拿捏；好在，写这些文字主要是为了将来碰到某些反直觉的情况时可以有个快捷解答；最后若能得到碰巧逛到这里的同仁指点迷津，纠正错误，互通有无，就算赚到了 :-) 希望读完此文，能够消除一些关于 EOF 的疑惑，再碰到关于她的一些争论时，大家能够相视一笑。 愿此文，能解释 什么是 EOF？ 为什么需要 EOF？ 文件里包不包含 EOF？ 终端输入时的 EOF 的表示方式和处理行为是怎么样的? 不同计算机语言的 EOF 如何定义的？ …… may your blade never dull section-0 概 …

阅读更多

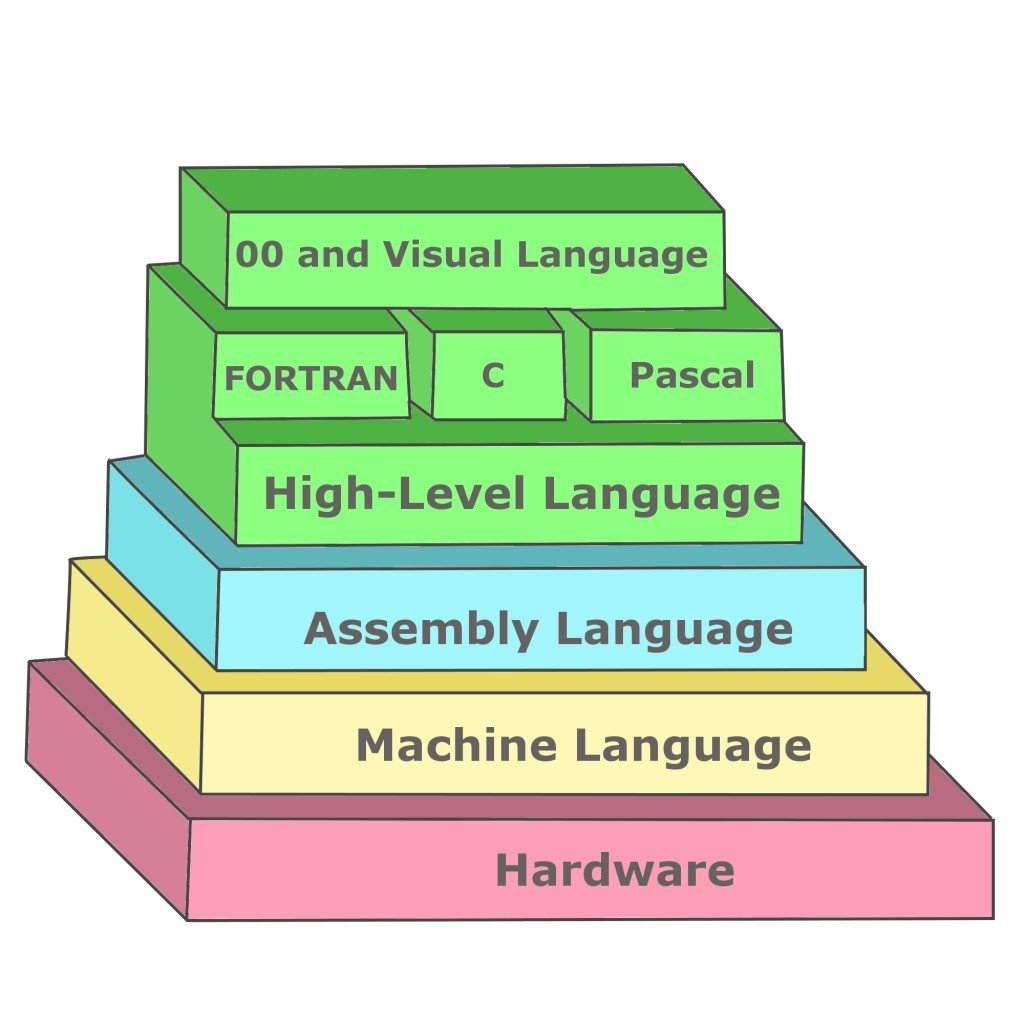
Index-0 原址：https://asmtutor.com/ 环境：nasm on x64 linux TL;DR 动机：程序员——多掌握几门计算机语言，还是有好处的 主题：汇编语言——有其不可替代的作用 呈示：天下语言逾千——汇编笑看沉舟侧畔 展开：欲知程序真相——反编译难，反汇编易 再现：大道器也不器——初见时如茶味甘苦，洞悉后若灌顶醍醐；原以为听多说多皆已昨，忽回首似曾相识又如陌；罢，风流不在谈峰健，相对无言味更长…… 原文作者自己说 『This project was put together to teach myself NASM assembly language on linux.』 欸~，原来是很窄众的哦。 写 …

阅读更多

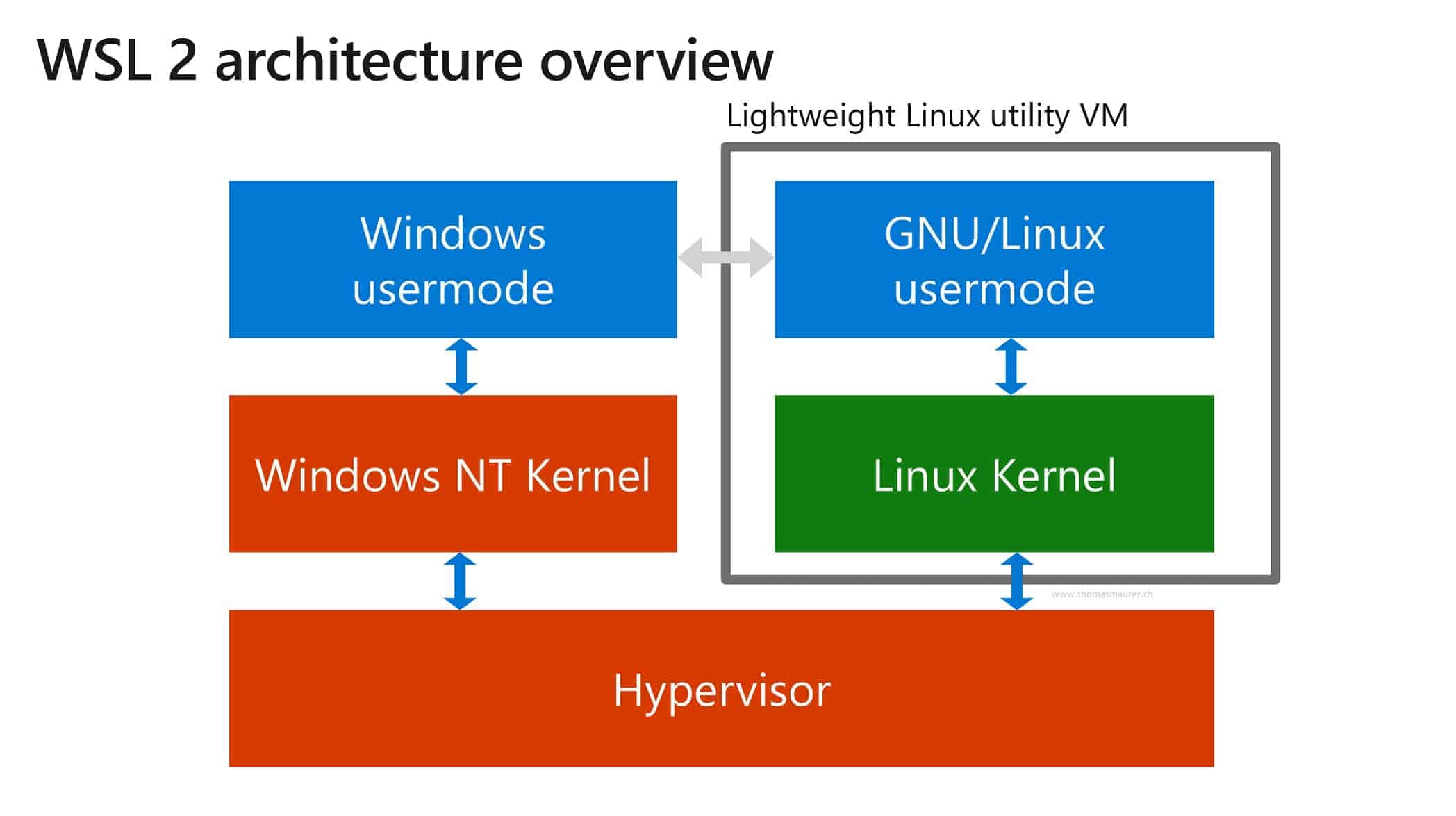
意图 备份还原 迁移 节省 C 盘空间 …… 步骤 导出 1wsl.exe --export <DistributionName> <FileName> 导入 1wsl.exe --import <DistributionName> <InstallLocation> <FileName> 提示：导入之后，执行 wsl -l -v 查看运行版本，如果是 1 的话，可以执行 wsl --set-version <DistributionName> 2 更新到 2 WSL 默认登录用户 如果迁移完毕后发现默认登录用户被置为：root，或者想要手动指定默认的登录用户，可以按如下操作设置： 注册表项： …

阅读更多

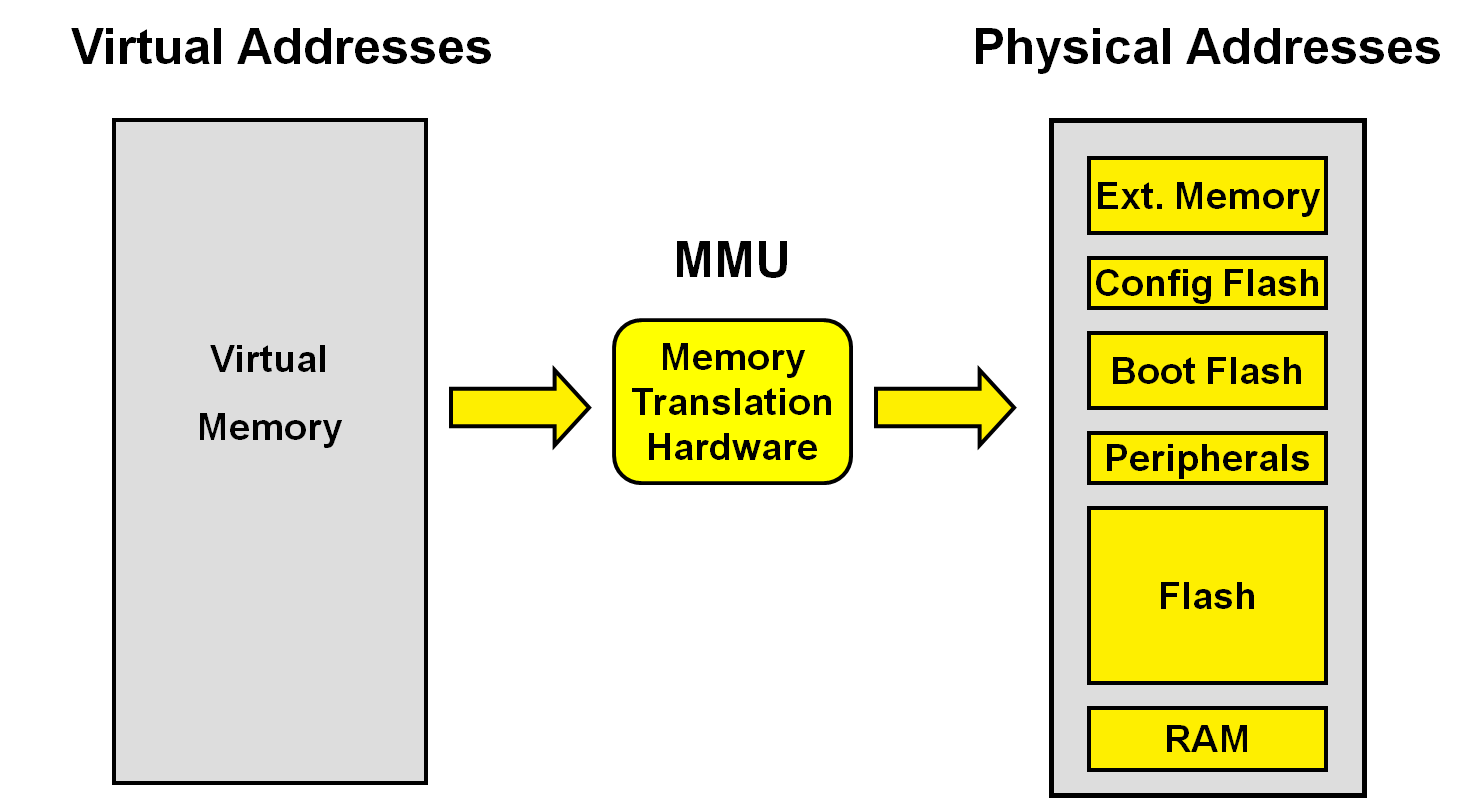
环境与条件：CPU 和操作系统都为 32 位，主存按字节编址 一、页大小的确定 一言以蔽之——在页表所占内存和页内填充内存的耗费上做取舍、折中 以下极端情况的对比，用以阐明为什么要取舍、折中 A、页面大小 = 1Byte 颗粒度到达极致细微、系统永远不必为页面填充不需要的内存 但页表项目达到 2^32 个，占用了整个内存 B、页面大小 = 4GBytes 每当新进程启动时，都需要将 4G 内存交换到磁盘 页表中只有一个条目，因此几乎不占用任何内存 因此： x86 设计人员发现 4K 大小的页面是很好的庸点 当然，随着 CPU 地址总线位数的扩张，系统中物理内存的膨胀，4K 也并不是总是合适的大小。 二、页大小 & 页内偏移量位数 已 …

阅读更多

GNU ed 手册 (version 1.16, 2020-02-20). 原址：https://www.gnu.org/software/ed/manual/ed_manual.html 概览: ed 概览 行编辑简介: GNU ed 起步 调用 ed: 命令行界面 行寻址: 在缓冲区中指定行/范围 正则表达式: 文本选择模式 命令: GNU ed 识别命令 限制: GNU ed 的固有局限性 诊断: GNU ed 错误处理 问题: 报告 bugs GNU Free Documentation License: How you can copy and share this manual Copyright © 1993, …

阅读更多

起因 gitlab 官方 docker 容器部署完毕。容器中的服务越少越好，所以使用外部 SMTP 发送邮件。 环境 撰写此文时： Docker 17.06.1-ce GitLab Community Edition 9.5.2 ab97415 步骤 网易 163 邮箱 授权码设置 协议开启与服务器地址 容器中的 /etc/gitlab/gitlab.rb 1### Email Settings 2# gitlab_rails['gitlab_email_enabled'] = true 3gitlab_rails['gitlab_email_from'] = '<yourname>@163.com' 4# …

阅读更多

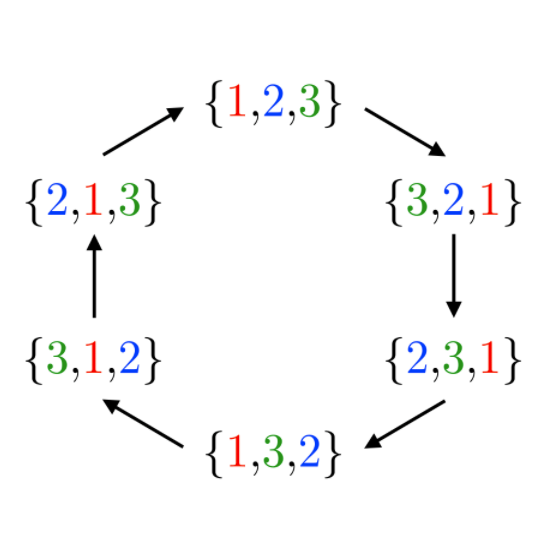
算法原理 相关算法——插入法 对于集合 $$ S={a_1, a_2, ..., a_n} $$ 若已知前 $n-1$ 个元素的全排列，则 $n$ 个元素的全排列 $$ p_i={p_1,p_2,...,p_{(n-1)!}} $$ 可以这样生成：将 $a_n$ 插入 $p_i$ 不同位置中，由此，得到集合 $S$ 的全排列 为什么这样操作能得到集合 $S$ 的全排列？因为每个 $p_i$ 的可能插入位置为 $n$ 个，所以总数是 $n!$ 又因为每个 $p_i$ 是不同的，因此，得到的排列必然没有重复 插入法有一个缺点：为了产生 $n$ 个元素的排列，必须知道并存储所有 $n-1$ 个元素的排列，然后才能产生出所有 $n$ …

阅读更多