邻位对换法生成全排列

Feb 2, 2017 · 4 min read · Math Algorithm Programming ·

算法原理

邻位对换法的改进

依赖插入法能够生成全排列的事实，但邻位对换法不需要知道 $n-1$ 个元素的排列，只需要从某一个初始排列状态开始，进行特定的相邻元素交换即可生成全排列

算法正确性

假设算法对 $n$ 个元素能生成全排列，只需要证明其对 $n+1$ 个元素，也能生成全排列，对于新进来的元素，将其认为值最大，插入最右方，每次从右移到左，或者改变方向后从左移到右，就可以认为对于一个排列从不同位置插入生成一个新的排列，而原本 $n$ 个元素是全排列的，因此对于 $n+1$ 个元素也是全排列的，因此邻位对换法能生成全排列

以 $S=\{1, 2, 3, 4\}$ 为例。若 $\{1, 2, 3\}$ 的全排列为：

$p_1$	$p_2$	$p_3$	$p_4$	$p_5$	$p_6$
123	132	312	321	231	213

那么，将 $4$ 按从尾到头的方式插入每一个排列，就得到：

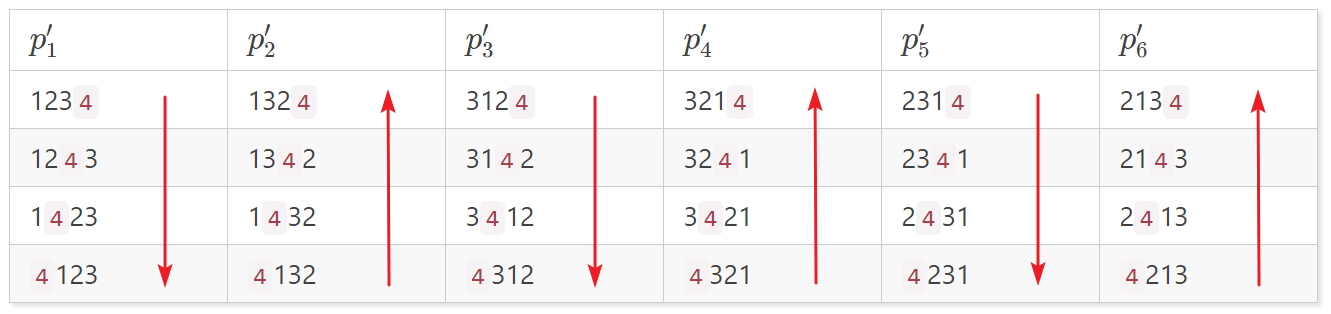
观察——

第 1 列，从上往下走
第 2 列，从下往上走
第 3 列，从上往下走
．．．
一直走到最后一列，当前方向上的最后一格

规律：路径上的任一排列是前一个排列交换两个相邻元素而得

比如 1423 ，它是由 1243 通过 4 与 2 换位得到

即：一个排列，由上一排列通过交换该排列下标为 $k-1$ 和 $k$ 的元素得到，越界的情况由突变解决。

算法步骤

在上面的模式中，交换的下标 $k$ 的序列为（设元素下标从左到右）：

3 2 1 {递减到1突变为3}
1 2 3 {递增到3突变为1}
3 2 1 {递减到1突变为3}
1 2 3 {递增到3突变为1}
3 2 1 {递减到1突变为3}
1 2 3

可以看到：对元素个数为 $n$ 的集合 $S$，其交换下标 $k, k \in [1,n-1]$ 的序列有如下规律：

1）开始时 $k = n-1$，每次减 $1$

2）当减到 $1$ 或加到 $n-1$ 时，$k$ 值发生突变：若前一个 $k = 1$，则变为 $n-1$；若前一个 $k = n-1$，则变为 $1$

3）$k$ 值突变后，新的 $k$ 以突变前的 $k$ 值开始递进（若是 $1$ 就递增，若是 $n-1$ 就递减）

4）$k$ 值突变后的交换下标序列是突变前的序列关于突变位置的“镜像”

比如：前 7 个交换下标 3 2 1 {3} 1 2 3 （加粗的位置为突变位置）
显然，突变位置后的下标 1 2 3 是突变前的下标 3 2 1 的"镜像"

根据如上规律，可编写相应的算法实现

代码实现

Java

 1import java.util.ArrayList;
 2
 3public class Permutation {
 4
 5    public static void main( String[] args ) {
 6        String[] result = permutation( "12345" );
 7        // System.out.println( result.length + "\r\n" );
 8        for ( String s : result ) {
 9            System.out.println( s );
10        }
11    }
12
13    public static String[] permutation( String str ) {
14
15        ArrayList<String> charList = new ArrayList<String>();
16        char[]            arrChars = str.toCharArray();
17        long              times    = 1;
18        int               k        = arrChars.length - 2;
19        int               inc      = -1;
20
21        for ( int i = 1; i < arrChars.length + 1; i++ ) {
22            times *= i;
23        }
24
25        for ( int i = 1; i < times; i++ ) {
26
27            swap( arrChars, k, k + 1 );
28            charList.add( new String( arrChars ) );
29            k += inc;
30
31            if ( k == -1 ) {
32                inc = 1;
33                k = 0;
34                swap( arrChars, arrChars.length - 2, arrChars.length - 1 );
35                charList.add( new String( arrChars ) );
36                i++;
37            }
38
39            if ( k == arrChars.length - 1 ) {
40                inc = -1;
41                k = arrChars.length - 2;
42                swap( arrChars, 0, 1 );
43                charList.add( new String( arrChars ) );
44                i++;
45            }
46        }
47
48        return charList.toArray( new String[0] );
49    }
50
51    private static void swap( char[] arr, int k1, int k2 ) {
52        char tmp = arr[k1];
53        arr[k1] = arr[k2];
54        arr[k2] = tmp;
55    }
56}

C++

 1#include <iostream>
 2#include <string>
 3#include <iterator>
 4#include <algorithm>
 5
 6using namespace std;
 7
 8#define _swap(a, b) { int t = a; a = b; b = t; }
 9
10void permutation(int n) {
11
12	long long times = 1;
13	int *list = new int[n], k = n - 2, maxK = n - 2, dir = -1 ;
14
15	for (long long i = 1; i < n; ++i)
16		times *= i, list[i - 1] = i;
17
18	list[n - 1] = n;
19	// copy(list, list + n, ostream_iterator<int>(cout, " ")), cout << endl;
20
21	for (long long i = 1; i <= times; ++i) {
22		for (int j = 0; j < n - 1; ++j) {
23			_swap(list[k], list[k + 1]);
24			// copy(list, list + n, ostream_iterator<int>(cout, " ")), cout << endl;
25			k += dir;
26		}
27		k = i & 1 ? maxK : 0;
28		_swap(list[k], list[k + 1]);
29		// copy(list, list + n, ostream_iterator<int>(cout, " ")), cout << endl;
30		k = maxK - k;
31		dir = -dir;
32	}
33
34	delete[]list;
35}
36
37int main() {
38	permutation(5);
39}

说明

实现相同功能的递归实现较多，但时间与空间复杂度高
不使用递归的代码看上去较多一点，但效能收益可观

参考

全排列生成算法

本文采用知识共享署名许可协议（CC-BY 4.0）进行许可，转载注明来源即可。如有错误劳烦评论或邮件指出。